FFT를 DSP를 사용해서 만들려고했더니 그냥 내가 만들고 쓰는게 좋을것 같다는 생각이 들었다.
하지만.... 귀찮자나... 구글링을 하여 참고했다.
C언어에 의한 디지털 신호 처리 입문 DSP(성안당)책의 예제를 수정했다.
FFT.h
#ifndef __FFT_H_
#define __FFT_H_
extern void fft_table(float wn_FFT[], short br_FFT[], int N_FFT);
extern void fft(float xR[], float xI[], float wn_FFT[], short br_FFT[], int N_FFT);
#endifFFT.c
/*********************/
/* Functions for FFT */
/*********************/
#include <math.h>
#include "FFT.h"
#define _2PI 6.28318530718f
static void swap(float *a, float *b);
/***************************/
/* Genarate tables for FFT */
/***************************/
void fft_table(float wn_FFT[], short br_FFT[], int N_FFT)
{
int n_half;
float arg;
/* Calculation of twiddle factor */
arg = _2PI / N_FFT;
for (int i = 0; i < ((N_FFT * 3) >> 2); i++) {
wn_FFT[i] = cosf(arg * i);
}
/* Calculation of bit reversal table */
n_half = N_FFT >> 1;
br_FFT[0] = 0;
for (int ne = 1; ne < N_FFT; ne = ne << 1) {
for (int jp = 0; jp < ne; jp++) {
br_FFT[jp + ne] = br_FFT[jp] + n_half;
}
n_half = n_half >> 1;
}
}
/**************************/
/* FFT for complex signal */
/**************************/
void fft(float xR[], float xI[], float wn_FFT[], short br_FFT[], int N_FFT)
{
float xtmpR, xtmpI;
int jnh, jxC, jxS, n_half, n_half2;
n_half = N_FFT >> 1;
for (int ne = 1; ne < N_FFT; ne = ne << 1) {
n_half2 = n_half<<1;
for (int k = 0; k < N_FFT; k = k + n_half2) {
jxC = 0;
jxS = N_FFT >> 2;
for (int j = k; j < (k + n_half); j++) {
jnh = j + n_half;
/* beginning of butterfly operations */
xtmpR = xR[j];
xtmpI = xI[j];
xR[j] = xtmpR + xR[jnh];
xI[j] = xtmpI + xI[jnh];
xtmpR = xtmpR - xR[jnh];
xtmpI = xtmpI - xI[jnh];
xR[jnh] = xtmpR * wn_FFT[jxC] - xtmpI * wn_FFT[jxS];
xI[jnh] = xtmpR * wn_FFT[jxS] + xtmpI * wn_FFT[jxC];
/* end of butterfly operations */
jxC = jxC + ne;
jxS = jxS + ne;
}
}
n_half = n_half>>1;
}
/* Bit reverse */
for (int j = 0; j < N_FFT; j++) {
if (j<br_FFT[j]) {
swap(&xR[j], &xR[br_FFT[j]]);
swap(&xI[j], &xI[br_FFT[j]]);
}
}
}
/* used in FFT procedure */
static void swap(float *a, float *b)
{
float tmp;
tmp = *a;
*a = *b;
*b = tmp;
}
그러면 이 fft가 정상적으로 돌고 있는지 확인이 필요하다.
FFT_main.c
/*****************************/
/* FFT test program, N = 256 */
/*****************************/
#include <stdio.h>
#include <math.h>
#include "FFT.h"
#define nFFT 256
#define nFFT3_4 ((nFFT*3)/4)
float wn_FFT[nFFT3_4]; /* for twiddle factor */
short br_FFT[nFFT]; /* for bit reversal */
float xr[nFFT], xi[nFFT], yr[nFFT], yi[nFFT]; // yr: 실수 부 yi: 허수 부
void main()
{
short i;
for (i=0; i<nFFT; i++)
{
xr[i] =sin(6.28*i/3);
}
fft_table(wn_FFT, br_FFT, nFFT); /* ganarate tables for FFT */
/* genarate rectangular wave */
for (i=0; i<nFFT; i++)
{
yr[i] = xr[i];
yi[i] = xi[i];
}
fft(yr, yi, wn_FFT, br_FFT, nFFT); /* FFT */
for(i=0;i<nFFT;i++)
{
printf("%d : %f \n",i, xr[i]);
}
printf("\n\n ");
for(i=0;i<nFFT;i++)
{
printf("%d : %f %f \n", i, yr[i], yi[i]);
}
}
빌드를 하기 위해서 간단한 스크립트가 필요하다. 명령어로 쳐도되지만 귀찮으니깐 작성한다.
make.sh
gcc -c FFT_main.c -lm
gcc -c FFT.c -lm -lc
gcc FFT_main.o FFT.o -o test.out -lm
자 이제 실행을 시켜본다. 아래와 같은 결과가 나온다.
0 : 0.000000
1 : 0.866556
2 : -0.864962
3 : -0.003185
4 : 0.868141
5 : -0.863359
6 : -0.006371
7 : 0.869718
8 : -0.861747
9 : -0.009556
10 : 0.871285
11 : -0.860127
12 : -0.012741
13 : 0.872844
14 : -0.858498
15 : -0.015926
16 : 0.874394
17 : -0.856860
18 : -0.019111
19 : 0.875935
20 : -0.855213
21 : -0.022295
22 : 0.877468
23 : -0.853558
24 : -0.025480
25 : 0.878991
26 : -0.851894
27 : -0.028664
28 : 0.880505
29 : -0.850222
30 : -0.031848
31 : 0.882011
32 : -0.848541
33 : -0.035031
34 : 0.883507
35 : -0.846851
36 : -0.038214
37 : 0.884995
38 : -0.845152
39 : -0.041397
40 : 0.886473
41 : -0.843446
42 : -0.044580
43 : 0.887943
44 : -0.841730
45 : -0.047761
46 : 0.889404
47 : -0.840006
48 : -0.050943
49 : 0.890855
50 : -0.838274
51 : -0.054124
52 : 0.892298
53 : -0.836532
54 : -0.057304
55 : 0.893731
56 : -0.834783
57 : -0.060484
58 : 0.895156
59 : -0.833025
60 : -0.063663
61 : 0.896571
62 : -0.831259
63 : -0.066842
64 : 0.897977
65 : -0.829484
66 : -0.070019
67 : 0.899374
68 : -0.827700
69 : -0.073197
70 : 0.900762
71 : -0.825909
72 : -0.076373
73 : 0.902141
74 : -0.824109
75 : -0.079549
76 : 0.903511
77 : -0.822300
78 : -0.082723
79 : 0.904871
80 : -0.820483
81 : -0.085897
82 : 0.906223
83 : -0.818658
84 : -0.089070
85 : 0.907565
86 : -0.816825
87 : -0.092243
88 : 0.908898
89 : -0.814983
90 : -0.095414
91 : 0.910221
92 : -0.813133
93 : -0.098584
94 : 0.911536
95 : -0.811275
96 : -0.101753
97 : 0.912841
98 : -0.809408
99 : -0.104922
100 : 0.914137
101 : -0.807534
102 : -0.108089
103 : 0.915424
104 : -0.805651
105 : -0.111255
106 : 0.916701
107 : -0.803760
108 : -0.114420
109 : 0.917969
110 : -0.801861
111 : -0.117584
112 : 0.919228
113 : -0.799953
114 : -0.120746
115 : 0.920478
116 : -0.798038
117 : -0.123908
118 : 0.921718
119 : -0.796115
120 : -0.127068
121 : 0.922949
122 : -0.794183
123 : -0.130227
124 : 0.924170
125 : -0.792243
126 : -0.133384
127 : 0.925382
128 : -0.790295
129 : -0.136540
130 : 0.926585
131 : -0.788340
132 : -0.139695
133 : 0.927778
134 : -0.786376
135 : -0.142848
136 : 0.928962
137 : -0.784404
138 : -0.146000
139 : 0.930136
140 : -0.782425
141 : -0.149151
142 : 0.931301
143 : -0.780437
144 : -0.152300
145 : 0.932457
146 : -0.778442
147 : -0.155447
148 : 0.933603
149 : -0.776438
150 : -0.158593
151 : 0.934739
152 : -0.774427
153 : -0.161737
154 : 0.935866
155 : -0.772408
156 : -0.164880
157 : 0.936984
158 : -0.770381
159 : -0.168021
160 : 0.938092
161 : -0.768346
162 : -0.171160
163 : 0.939191
164 : -0.766303
165 : -0.174297
166 : 0.940280
167 : -0.764253
168 : -0.177433
169 : 0.941359
170 : -0.762195
171 : -0.180567
172 : 0.942429
173 : -0.760129
174 : -0.183699
175 : 0.943490
176 : -0.758055
177 : -0.186829
178 : 0.944540
179 : -0.755974
180 : -0.189957
181 : 0.945582
182 : -0.753885
183 : -0.193083
184 : 0.946613
185 : -0.751789
186 : -0.196208
187 : 0.947635
188 : -0.749684
189 : -0.199330
190 : 0.948648
191 : -0.747573
192 : -0.202451
193 : 0.949651
194 : -0.745453
195 : -0.205569
196 : 0.950644
197 : -0.743326
198 : -0.208685
199 : 0.951627
200 : -0.741192
201 : -0.211799
202 : 0.952601
203 : -0.739050
204 : -0.214911
205 : 0.953565
206 : -0.736900
207 : -0.218021
208 : 0.954520
209 : -0.734743
210 : -0.221129
211 : 0.955465
212 : -0.732579
213 : -0.224234
214 : 0.956400
215 : -0.730407
216 : -0.227337
217 : 0.957325
218 : -0.728227
219 : -0.230438
220 : 0.958241
221 : -0.726041
222 : -0.233536
223 : 0.959147
224 : -0.723847
225 : -0.236632
226 : 0.960043
227 : -0.721645
228 : -0.239726
229 : 0.960930
230 : -0.719437
231 : -0.242817
232 : 0.961807
233 : -0.717220
234 : -0.245906
235 : 0.962674
236 : -0.714997
237 : -0.248992
238 : 0.963531
239 : -0.712767
240 : -0.252076
241 : 0.964379
242 : -0.710529
243 : -0.255157
244 : 0.965216
245 : -0.708284
246 : -0.258235
247 : 0.966044
248 : -0.706032
249 : -0.261311
250 : 0.966862
251 : -0.703772
252 : -0.264385
253 : 0.967671
254 : -0.701506
255 : -0.267455
0 : -0.123198 0.000000
1 : -0.123126 -0.007930
2 : -0.122908 -0.015862
3 : -0.122544 -0.023806
4 : -0.122035 -0.031764
5 : -0.121380 -0.039740
6 : -0.120572 -0.047741
7 : -0.119615 -0.055772
8 : -0.118511 -0.063836
9 : -0.117249 -0.071941
10 : -0.115835 -0.080087
11 : -0.114259 -0.088290
12 : -0.112521 -0.096542
13 : -0.110621 -0.104855
14 : -0.108549 -0.113239
15 : -0.106304 -0.121693
16 : -0.103885 -0.130227
17 : -0.101283 -0.138847
18 : -0.098494 -0.147560
19 : -0.095510 -0.156371
20 : -0.092329 -0.165291
21 : -0.088945 -0.174320
22 : -0.085341 -0.183480
23 : -0.081518 -0.192765
24 : -0.077469 -0.202191
25 : -0.073179 -0.211767
26 : -0.068640 -0.221501
27 : -0.063844 -0.231406
28 : -0.058776 -0.241489
29 : -0.053424 -0.251766
30 : -0.047775 -0.262245
31 : -0.041814 -0.272944
32 : -0.035529 -0.283874
33 : -0.028899 -0.295053
34 : -0.021904 -0.306495
35 : -0.014527 -0.318217
36 : -0.006745 -0.330241
37 : 0.001467 -0.342586
38 : 0.010130 -0.355269
39 : 0.019280 -0.368319
40 : 0.028942 -0.381763
41 : 0.039150 -0.395626
42 : 0.049946 -0.409938
43 : 0.061363 -0.424732
44 : 0.073453 -0.440049
45 : 0.086258 -0.455923
46 : 0.099838 -0.472400
47 : 0.114251 -0.489527
48 : 0.129560 -0.507363
49 : 0.145845 -0.525959
50 : 0.163184 -0.545389
51 : 0.181668 -0.565716
52 : 0.201407 -0.587032
53 : 0.222508 -0.609419
54 : 0.245117 -0.633001
55 : 0.269366 -0.657869
56 : 0.295433 -0.684170
57 : 0.323507 -0.712053
58 : 0.353817 -0.741692
59 : 0.386610 -0.773293
60 : 0.422188 -0.807076
61 : 0.460893 -0.843320
62 : 0.503130 -0.882337
63 : 0.549379 -0.924502
64 : 0.600205 -0.970254
65 : 0.656288 -1.020123
66 : 0.718448 -1.074750
67 : 0.787686 -1.134913
68 : 0.865234 -1.201563
69 : 0.952626 -1.275900
70 : 1.051803 -1.359426
71 : 1.165236 -1.454065
72 : 1.296161 -1.562323
73 : 1.448846 -1.687514
74 : 1.629088 -1.834138
75 : 1.844934 -2.008431
76 : 2.107881 -2.219318
77 : 2.435001 -2.480033
78 : 2.852723 -2.811070
79 : 3.404269 -3.245944
80 : 4.165568 -3.843529
81 : 5.283331 -4.717576
82 : 7.082648 -6.120130
83 : 10.456424 -8.743481
84 : 19.066139 -15.426424
85 : 87.063713 -68.153641
86 : -36.511555 27.647909
87 : -15.552743 11.390221
88 : -10.065076 7.127387
89 : -7.538008 5.159824
90 : -6.085839 4.025509
91 : -5.143856 3.286615
92 : -4.484010 2.766313
93 : -3.996549 2.379519
94 : -3.622139 2.080224
95 : -3.325882 1.841359
96 : -3.085931 1.645970
97 : -2.887883 1.482898
98 : -2.721882 1.344487
99 : -2.580951 1.225317
100 : -2.460001 1.121436
101 : -2.355250 1.029906
102 : -2.263824 0.948480
103 : -2.183496 0.875426
104 : -2.112511 0.809372
105 : -2.049484 0.749233
106 : -1.993293 0.694125
107 : -1.943035 0.643328
108 : -1.897934 0.596244
109 : -1.857391 0.552379
110 : -1.820886 0.511319
111 : -1.787978 0.472701
112 : -1.758300 0.436226
113 : -1.731541 0.401633
114 : -1.707435 0.368694
115 : -1.685756 0.337210
116 : -1.666304 0.307005
117 : -1.648912 0.277921
118 : -1.633445 0.249835
119 : -1.619770 0.222601
120 : -1.607789 0.196115
121 : -1.597405 0.170272
122 : -1.588552 0.144976
123 : -1.581159 0.120143
124 : -1.575178 0.095673
125 : -1.570567 0.071505
126 : -1.567295 0.047549
127 : -1.565343 0.023740
128 : -1.564691 0.000000
129 : -1.565341 -0.023737
130 : -1.567296 -0.047546
131 : -1.570567 -0.071502
132 : -1.575178 -0.095673
133 : -1.581159 -0.120138
134 : -1.588552 -0.144973
135 : -1.597409 -0.170270
136 : -1.607789 -0.196114
137 : -1.619775 -0.222599
138 : -1.633446 -0.249835
139 : -1.648917 -0.277928
140 : -1.666304 -0.307005
141 : -1.685757 -0.337210
142 : -1.707437 -0.368693
143 : -1.731541 -0.401633
144 : -1.758300 -0.436226
145 : -1.787978 -0.472700
146 : -1.820885 -0.511317
147 : -1.857393 -0.552381
148 : -1.897933 -0.596244
149 : -1.943022 -0.643333
150 : -1.993297 -0.694121
151 : -2.049486 -0.749230
152 : -2.112512 -0.809371
153 : -2.183495 -0.875422
154 : -2.263825 -0.948477
155 : -2.355257 -1.029904
156 : -2.460002 -1.121435
157 : -2.580950 -1.225314
158 : -2.721885 -1.344483
159 : -2.887887 -1.482896
160 : -3.085932 -1.645969
161 : -3.325887 -1.841357
162 : -3.622141 -2.080221
163 : -3.996554 -2.379521
164 : -4.484012 -2.766312
165 : -5.143863 -3.286612
166 : -6.085843 -4.025506
167 : -7.538015 -5.159823
168 : -10.065078 -7.127385
169 : -15.552751 -11.390216
170 : -36.511562 -27.647890
171 : 87.063744 68.153595
172 : 19.066143 15.426414
173 : 10.456430 8.743471
174 : 7.082649 6.120126
175 : 5.283337 4.717570
176 : 4.165569 3.843528
177 : 3.404271 3.245943
178 : 2.852723 2.811067
179 : 2.435005 2.480033
180 : 2.107883 2.219317
181 : 1.844936 2.008430
182 : 1.629088 1.834137
183 : 1.448848 1.687513
184 : 1.296160 1.562322
185 : 1.165239 1.454065
186 : 1.051802 1.359426
187 : 0.952632 1.275898
188 : 0.865236 1.201563
189 : 0.787689 1.134913
190 : 0.718447 1.074750
191 : 0.656288 1.020125
192 : 0.600205 0.970254
193 : 0.549378 0.924500
194 : 0.503130 0.882338
195 : 0.460890 0.843318
196 : 0.422188 0.807077
197 : 0.386612 0.773292
198 : 0.353815 0.741692
199 : 0.323509 0.712052
200 : 0.295434 0.684169
201 : 0.269367 0.657866
202 : 0.245116 0.632996
203 : 0.222514 0.609429
204 : 0.201408 0.587035
205 : 0.181671 0.565723
206 : 0.163183 0.545387
207 : 0.145846 0.525962
208 : 0.129561 0.507363
209 : 0.114249 0.489531
210 : 0.099838 0.472399
211 : 0.086257 0.455925
212 : 0.073452 0.440050
213 : 0.061363 0.424744
214 : 0.049946 0.409935
215 : 0.039152 0.395625
216 : 0.028943 0.381762
217 : 0.019280 0.368319
218 : 0.010133 0.355268
219 : 0.001466 0.342584
220 : -0.006744 0.330240
221 : -0.014528 0.318216
222 : -0.021904 0.306493
223 : -0.028898 0.295054
224 : -0.035530 0.283874
225 : -0.041817 0.272945
226 : -0.047776 0.262244
227 : -0.053426 0.251765
228 : -0.058776 0.241488
229 : -0.063843 0.231405
230 : -0.068643 0.221500
231 : -0.073181 0.211766
232 : -0.077468 0.202192
233 : -0.081520 0.192766
234 : -0.085341 0.183476
235 : -0.088943 0.174330
236 : -0.092329 0.165291
237 : -0.095512 0.156376
238 : -0.098494 0.147560
239 : -0.101280 0.138848
240 : -0.103885 0.130228
241 : -0.106304 0.121694
242 : -0.108547 0.113237
243 : -0.110619 0.104860
244 : -0.112520 0.096542
245 : -0.114257 0.088292
246 : -0.115832 0.080085
247 : -0.117251 0.071940
248 : -0.118511 0.063837
249 : -0.119617 0.055771
250 : -0.120571 0.047742
251 : -0.121381 0.039741
252 : -0.122036 0.031764
253 : -0.122546 0.023806
254 : -0.122907 0.015862
255 : -0.123127 0.007929
그러면 결과값이 맞는지 확인이 필요하니 엑셀로 옮긴다.

이렇게 일단 정리를 했다 그러면 excel에서 complex를 구한다.

위와 같이 분석도구가 활성화 되어있다면

데이터 분석을 키고

푸리에분석을 확인을 누르면

위와같이 입력후 확인을 누른다.
둘다 86Hz에서 튀어있는걸 볼 수 있다.
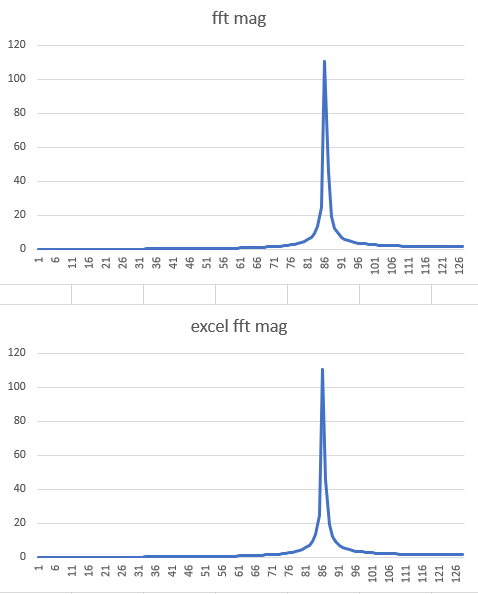
그럼 계산을 해보면

85.3Hz주기의 주파수 대역이니 정상적인 주파수 대역이 맞고,

두 값도 일치한다.
정상적인 코드가 맞는지 확인이 완료되었으니 사용이 가능하다.
해당 excel 파일은 첨부한다.
'FW' 카테고리의 다른 글
| stm32 HAL timer(2) (0) | 2021.12.04 |
|---|---|
| stm32 HAL timer(1) (0) | 2021.10.30 |
| IAR Heap Stack size 조절 (0) | 2021.09.19 |
| Hanning window (0) | 2021.09.19 |
| IAR CMSIS DSP Library사용 (0) | 2021.08.21 |